フェボナチ・ゴールデンレイシオ
【ステンレス】
サイズ:54mm×33mm
※レーザーで切り出しているため、お部屋にテグスで吊るしたり、丸カンを付けることでアクセサリー加工も可能です。
フェボナチ・ゴールデンレイシオ
フィボナッチ数列が興味深いのは、黄金比との関わりでしょう。そして、自然界にフィボナッチ数列・黄金比と関わりのある事象がたくさんあるということです。こ古代ギリシャのピタゴラスとユークリッドから、ピサの中世イタリアの数学者レオナルドとルネッサンスの天文学者ヨハネス・ケプラーまで、オックスフォードの物理学者ロジャー・ペンローズのような現代の科学者まで、多くの人たちがこの二つの関係性の研究に多くの時間を費やしてきました。生物学者、芸術家、ミュージシャン、歴史家、建築家、心理学者、さらには神秘学者は、その普遍性と魅力の基礎を研究し、議論してきました。
神聖幾何学の根本原理、調和という美しさの象徴と言えるでしょう。
高いレベルのヒーリングに強いかかわりを見出す人も少なくありません。
フィボナッチ数列(Fibonacci sequence)は、イタリアの数学者レオナルド・フィボナッチ(ピサのレオナルド)に因んで名付けられた数列です。1202年にフィボナッチが発行した『算盤の書』(Liber Abaci) に記載されたことで「フィボナッチ数」と呼ばれていますが、それ以前にインドの学者であるヘーマチャンドラ (Hemachandra) が韻律の研究により発見し、書物に記したことがわかっています。
神聖幾何学は宇宙の原理を表す言語といわれます。また、ガリレオ・ガリレイは「自然という書物は数学の言葉で書かれている」と言いました。
フェボナッチ数列を漸化式で表すと下記になります。
F0 = 0,
F1 = 1,
Fn+2 = Fn + Fn+1 (n ≥ 0)
普通の人間には何やらわけがわかりません。
しかし、、実際のその数列を見るとその規則ルールはとても簡単でだれでもわかります。
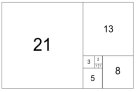
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …
左隣の数を足して次の数字を求めているのです。
0+1=1, 1+1=2, 1+2=3、 2+3=5, 3+5=8, 5+8=13, 8+13=21 ・・・・
このような形で続いていきます。
このフェボナッチ数列は、ヒマワリの種、松ぼっくり、サボテンのとげ、またいろいろな花のビラの数にも表れます。
〜フェボナッチ数列と黄金比〜
1,1,2,3,5,8,13,21,34,55,89,144,233,・・・・・・
このフェボナッチ数列のとなり合う2数の比を分数の形にならべて新しい数列をつくります。
1/1、2/1、3/2、5/3、8/5、13/8、21/13、34/21、89/55、144/89、233/144・・・・・
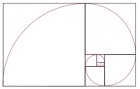
実はこのフェボナッチ数列の隣り合う二つの数の日は、黄金比に限りなく近づいています。
自然界のあらゆるところにちりばめられた、フェボナッチ数列
そして、この世界で最も調和的で美しい比率である黄金比
それが関わりっており、それは、自然の調和、あるいは原則のすべてを物語っているともいえるかもしれません。